

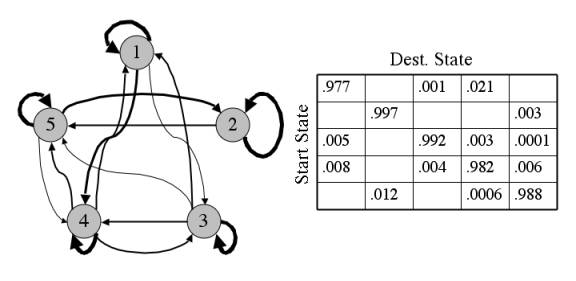
Under conditional dependence, the probability of heads on the next flip is 0.0009765625 * 0.5 = 0.00048828125. So imagine after 10 flips we have a random sequence of heads and tails. The joint probability of that sequence is 0.5^10 = 0.0009765625. Under the assumption of conditional dependence (the coin has memory of past states and the future state depends on the sequence of past states) we must record the specific sequence that lead up to the 11th flip and the joint probabilities of those flips. Suspend disbelief and assume that the Markov property is not yet known and we would like to predict the probability of flipping heads after 10 flips. ".a random process where the future is independent of the past given the present." Īssume a simplified coin toss game with a fair coin. Two of the most well known applications were Brownian motion , and random walks. Markov chains are widely applicable to physics, economics, statistics, biology, etc. During his research Markov was able to extend the law of large numbers and the central limit theorem to apply to certain sequences of dependent random variables, now known as Markov Chains . The focus of his early work was number theory but after 1900 he focused on probability theory, so much so that he taught courses after his official retirement in 1905 until his deathbed. Markov was a Russian mathematician best known for his work on stochastic processes. A Hidden Markov Model for Regime Detection


 0 kommentar(er)
0 kommentar(er)
